Relate
Method
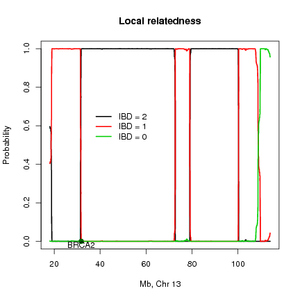
This method estimates the probability of sharing alleles identity by descent (IBD) across the genome and can also be used for mapping disease loci using distantly related individuals. These individuals will often be seemingly unrelated but if they share the same founder mutation then they will be distantly related. The method is based on a continuous time Markov model with hidden states. The hidden states are the IBD states between a pair of individuals with diploid chromosome. We assume that the individuals are not inbreed and thus the individuals can share 0, 1 or 2 alleles IBD. The SNPs are allowed to be in linkage disequilibrium (LD). To accommodate LD the methods need SNP for several individuals in order to estimate the allele frequencies and the pairwise LD. The method return the posterior probabilities of the IBD states across the genome and the overall IBD sharing. The estimates for all pairs of individuals can be combined info a score that will show linkage peaks across the genome and using a permutation procedure a significance threshold can be set. I recommend using the R package for fast visualization of a single pair of individuals (see figure).
Download and Installation
I move all the code to github [1]
Manual
See the manual.pdf in the download for in-depth information about installation, method and examples.
If you have any problems or comments please contact me albrecht @ binf.ku.dk
Citation
Anders Albrechtsen, Thorfinn Sand Korneliussen, Ida Moltke, Thomas van Overeem Hansen, Finn Cilius Nielsen, Rasmus Nielsen. Relatedness mapping and tracts of relatedness for genome-wide data in the presence of linkage disequilibrium. Genet Epidemiol. 2009 Apr;33(3):266-74
- Bibtex
% 19025785
@Article{pmid19025785,
Author="Albrechtsen, A. and Sand Korneliussen, T. and Moltke, I. and van Overeem Hansen, T.
and Nielsen, F. C. and Nielsen, R. ",
Title="{{R}elatedness mapping and tracts of relatedness for genome-wide data in the presence of linkage disequilibrium}",
Journal="Genet. Epidemiol.",
Year="2009",
Volume="33",
Number="3",
Pages="266--274",
Month="Apr"
}
- pubmed
table 1
There is an error in table 1 in the article. It should have said
| AA AA | |||
| AA aa | |||
| AA Aa | |||
| Aa Aa |
The difference in the 4 shown in bold
Change log
- Version 0.9993
Version for R 3+
- Version 0.997
- fixed a rare underflow problem fixed a problem for R version 2.15
- Version 0.995
- Removed some NAMESPACE stuff that did not work on 2.13.0
- Version 0.993 (3 april 2010)
- added another linkage example with plot
- Version 0.992 (18 jan 2010)
- made compatable with gcc 4.4.1
- Version 0.99 (12. april)
- Yet another fantastic release!
- Program uses much less memory know, and various bugs has been written. (See CHANGELOG in package for elaborate info)
- The manual has been updated.
- version 0.987 (24. feb 2009)
- A milestone release! This version has been very much anticipated
- Program can read plink binary files (R & commandline)
- Program can read pedfiles,using the 'snpMatrix' package (R only)
- Testfiles and examples are included
- A thoroughly manual is included, or can be downloaded here manual.pdf
- (subversion 0.98* are bugfixes for 0.98)
- version 0.95
- Much faster when performing linkage analysis in the C++ inplimentation (all pairs)
- If chromsome number is given the programs sorts the SNP accordenly
- version 0.83
- version 0.802
- apparantly the uint datatype doesn't exist in older compilers, So now a macro is added that defines the unsigned int if the gcc is older than 4.3













