|
|
| (57 intermediate revisions by 2 users not shown) |
| Line 4: |
Line 4: |
| The great thing about NGSadmix is that it is a new method that takes the uncertainty introduced in NGS sequencing data into account when inferring an individual's ancestry by using genotype likelihoods that considers the uncertainty caused by unobserved genotypes. | | The great thing about NGSadmix is that it is a new method that takes the uncertainty introduced in NGS sequencing data into account when inferring an individual's ancestry by using genotype likelihoods that considers the uncertainty caused by unobserved genotypes. |
|
| |
|
| REMEMBER TO EDIT AND CITE: "NGSadmix is only sensitive to admixture recent enough to cause structures in the population in terms of differing allele frequencies. Historical admixture events after which many generations has passed in the population, leaves no signature in terms of systematic differences in allele frequencies between individuals and are not a concern in association studies. "
| | As with the other existing software, ADMIXTURE and STRUCTURE, NGSadmix is only sensitive to admixture recent enough to cause structures in the population in terms of differing allele frequencies. Historical admixture events after which many generations has passed in the population, leaves no signature in terms of systematic differences in allele frequencies between individuals and are not a concern in association studies. |
| ADD ADMIXTURE AND STRUCTURE AS
| |
|
| |
|
| [[File:NgsAdmix.png|thumb]] | | [[File:NgsAdmix.png|thumb]] |
| Line 11: |
Line 10: |
| The method was published in 2013 and can be found here: [http://www.ncbi.nlm.nih.gov/pubmed/24026093] | | The method was published in 2013 and can be found here: [http://www.ncbi.nlm.nih.gov/pubmed/24026093] |
|
| |
|
| ==Citation==
| |
|
| |
| http://www.genetics.org/content/early/2013/09/03/genetics.113.154138.full.pdf
| |
|
| |
| Skotte, L., Korneliussen, T. S., & Albrechtsen, A. (2013). Estimating individual admixture proportions from next generation sequencing data. Genetics, 195(3), 693–702. doi:10.1534/genetics.113.154138
| |
|
| |
| :<u>'''Bibtex'''</u>
| |
| :% 24026093
| |
| :@Article{pmid24026093,
| |
| : Author="Skotte, L. and Korneliussen, T. S. and Albrechtsen, A. ",
| |
| : Title="{{E}stimating {I}ndividual {A}dmixture {P}roportions from {N}ext {G}eneration {S}equencing {D}ata}",
| |
| : Journal="Genetics",
| |
| : Year="2013",
| |
| : Pages=" ",
| |
| : Month="Sep"
| |
| :}
| |
|
| |
|
| ==Software Download== | | ==Software Download== |
| Line 41: |
Line 24: |
| NGSadmix can be installed independently or as a part of ANGSD. | | NGSadmix can be installed independently or as a part of ANGSD. |
|
| |
|
| ===NGSadmix Independent Installation=== | | ====NGSadmix Independent Installation==== |
|
| |
|
| 1. Login to your server using ssh on your terminal window. | | 1. Login to your server using ssh on your terminal window. |
| Line 55: |
Line 38: |
| :<code>g++ ngsadmix32.cpp -O3 -lpthread -lz -o NGSadmix</code> | | :<code>g++ ngsadmix32.cpp -O3 -lpthread -lz -o NGSadmix</code> |
|
| |
|
| 5. Delete source code to save space:
| | ====NGSadmix Installation from ANGSD==== |
| :<code>rm ~/Software/ngsadmix32.cpp</code>
| | |
| | :NGSadmix is part of the package ANGSD. To install ANGSD, please follow the instructions here [http://popgen.dk/angsd/index.php/Installation] |
| | |
| | ==Parameters== |
| | |
| | All parameters are set using '''-par value'''. |
| | For example, to get additional information, you would write '''-printInfo 1'''. |
|
| |
|
| ===NGSadmix Installation from ANGSD===
| | <pre>./NGSadmix </pre> |
|
| |
|
| <pre>
| | Arguments: |
| </pre>
| | |
| | ::'''-likes''' .beagle format filename with genotype likelihoods |
|
| |
|
| | ::'''-K''' Number of ancestral populations |
|
| |
|
| ==Run command example==
| | Optional: |
|
| |
|
| Download the input file
| | ::'''-fname''' Ancestral population frequencies |
| ::<code>wget popgen.dk/software/download/NGSadmix/data/input.gz</code> | |
|
| |
|
| Execute NGSadmix
| | ::'''-qname''' Admixture proportions |
| ::<code>./NGSadmix -likes input.gz -K 3 -P 4 -o myoutfiles -minMaf 0.05</code> | |
|
| |
|
| ===Detailed Examples and Tutorial===
| | ::'''-outfiles''' Prefix for output files |
|
| |
|
| Please refer to the tutorial's page [http://www.popgen.dk/software/index.php/NgsAdmixTutorial]
| | ::'''-printInfo''' print ID and mean maximum allele frequency (maf) for the SNPs that were analysed |
|
| |
|
| ==Parameters==
| | Setup: |
|
| |
|
| <div class="toccolours mw-collapsible mw-collapsed">
| | ::'''-seed''' Seed for initial guess in EM algorithm (a number lower than 1M is preferred). |
| | :: The same seed can be used to reproduce the analysis, and 3 different seeds can be used to test convergence. |
|
| |
|
| ./NGSadmix
| | ::'''-P''' Number of threads |
|
| |
|
| <pre class="mw-collapsible-content">
| | ::'''-method''' 0 indicates no acceleration of EM algorithm. Please refer to the paper for more information. |
|
| |
|
| *** see doc for options/possible ranges/ and further explanation
| | ::'''-misTol''' Tolerance for considering a site as missing. Default = 0.05. |
| | :: To include high quality genotypes only, increase this value (for example, 0.9) |
|
| |
|
| Arguments:
| |
| -likes .beagle format filename with genotype likelihoods
| |
| -K Number of ancestral populations
| |
| Optional:
| |
| -fname Ancestral population frequencies
| |
| -qname Admixture proportions
| |
| -outfiles Prefix for output files
| |
| -printInfo print ID and mean maf for the SNPs that were analysed
| |
| Setup:
| |
| -seed Seed for initial guess in EM
| |
| -P Number of threads
| |
| -method If 0 no acceleration of EM algorithm
| |
| -misTol Tolerance for considering site as missing
| |
| Stop criteria: | | Stop criteria: |
| -tolLike50 Loglikelihood difference in 50 iterations
| |
| -tol Tolerance for convergence
| |
| -dymBound Use dymamic boundaries (1: yes (default) 0: no)
| |
| -maxiter Maximum number of EM iterations
| |
| Filtering
| |
| -minMaf Minimum minor allele frequency
| |
| -minLrt Minimum likelihood ratio value for maf>0
| |
| -minInd Minumum number of informative individuals
| |
|
| |
|
| NB All parameters are set using '''-par value'''. So to get additional information you would write '''-printInfo 1'''.
| | ::'''-tolLike50''' Loglikelihood difference in 50 iterations. Default= 0.1 |
| | |
| | ::'''-tol''' Tolerance for convergence. Default = 1x10<sup>-5</sup>. Use maller values for higher accuracy. |
| | :: It's the maximum squared difference of F and Q (please refer to the paper for formula). |
|
| |
|
| </pre>
| | ::'''-dymBound''' Use dymamic boundaries (1: yes (default) 0: no). |
| </div>
| | |
| | |
| | ::'''-maxiter''' Maximum number of EM iterations. Default = 2000 (high value). |
| | :: In case it doesn't converge, this value needs to be higher. |
| | |
| | Filtering: |
| | |
| | ::'''-minMaf''' Minimum minor allele frequency. Default = 5% |
| | |
| | ::'''-minLrt''' Minimum likelihood ratio value for maf>0. Default = 0 |
| | |
| | ::'''-minInd''' Minumum number of informative individuals. Default = 0 |
| | :: It only keeps sites where there is at least x # of individuals with NGS data. |
|
| |
|
| ==Input File== | | ==Input File== |
| Input files are contains genotype likelihoods in genotype likelihood beagle input file format [http://faculty.washington.edu/browning/beagle/beagle.html]. We recommend [[ANGSD]] for easy transformation of Next-generation sequencing data to beagle format. See [http://www.popgen.dk/angsd/index.php/Beagle_input Creation of Beagle files with ANGSD]
| |
|
| |
|
| Example of a beagle genotype likelihood input file for 3 individuals.
| | The input file contains genotype likelihoods in a .beagle file format [http://faculty.washington.edu/browning/beagle/beagle.html]. |
| | and can be compressed with gzip. |
| | === BAM files === |
| | If you have BAM files you can use [[ANGSD]] to produce genotype likelihoods in .beagle format. Please |
| | see [http://www.popgen.dk/angsd/index.php/Beagle_input Creation of Beagle files with ANGSD] |
| | |
| | === VCF files === |
| | If you already have made a VCF file that contains genotype likehood information then it should be possible to convert .vcf files with genotype likelihoods to .beagle file via vcftools [https://vcftools.github.io/man_latest.html] |
| | |
| <pre> | | <pre> |
| marker allele1 allele2 Ind0 Ind0 Ind0 Ind1 Ind1 Ind1 Ind2 Ind2 Ind2
| | vcftools --vcf input.vcf --out test --BEAGLE-GL --chr 1,2 |
| 1_14000023 1 0 0.941 0.058 0.000 0.799 0.199 0.001 0.666 0.333 0.001
| |
| 1_14000072 2 3 0.709 0.177 0.112 0.941 0.058 0.000 0.665 0.332 0.001
| |
| 1_14000113 0 2 0.855 0.106 0.037 0.333 0.333 0.333 0.799 0.199 0.000
| |
| 1_14000202 2 0 0.835 0.104 0.060 0.799 0.199 0.000 0.333 0.333 0.333
| |
| ...
| |
| </pre> | | </pre> |
| Column 1:The marker name (the information is not atually used)
| | Chromosome has to be specified. |
|
| |
|
| Column 2 and 3: the major and minor allele (these two columns are not used within the program and can contain whatever dummy value).
| | You can also use bcftools' [https://samtools.github.io/bcftools/bcftools.html] 'query' option for generating a .beagle file from a .vcf file. |
|
| |
|
| The rest of the colums are the genotypes likelihoods (not in log space). For each individual we have 3 columns. | | ==Output Files== |
| Note that the above values sum to one per sites for each individuals. This is just a normalization of the genotype likelihoods in order to avoid underflow problems in the beagle software it does not mean that they are genotype probabilities.
| | The analysis performed by NGSadmix produces 4 files: |
|
| |
|
| The input file is allowed to be compressed with gzip. | | * Log likelihood of the estimates: a .log file that summarizes the run. The Command line used for running the program, what the likelihood is every 50 iterations, and finally how long it took to do the run. |
|
| |
|
| ==Output Files== | | * Estimated allele frequency: a zipped .fopt file, that contains an estimate of the allele frequency in each of the 3 assumed ancestral populations. There is a line for each locus. |
| Program outputs 3 files.
| | |
| | * Estimated admixture proportions: a .qopt file, that contains an estimate of the individual's ancestry proportion (admixture) from each of the three assumed ancestral populations for all individuals. There is a line for each individual. |
| | |
| | ==Run command example== |
|
| |
|
| # PREFIX.log
| | Download the input file, for example |
| # PREFIX.fopt.gz
| | ::<code>wget popgen.dk/software/download/NGSadmix/data/input.gz</code> |
| # PREFIX.qopt
| |
|
| |
|
| * The .log file contains log information of the run. Commandline used for running the program, what the likelihood is every 50 iterations, and finally how long it took to do the run.
| | Execute NGSadmix |
| | ::<code>./NGSadmix -likes input.gz -K 3 -P 4 -o myoutfiles -minMaf 0.05</code> |
|
| |
|
| * The .fopt.gz file is an compressed file, which contains an estimate of the frequency for each site for all populations. | | ::* '''-likes''' Input .beagle file of genotype likelihoods = input.gz |
| | ::* '''-K''' Ancestral populations K=3 |
| | ::* '''-P''' Number of threads used, as computer cores = 4 |
| | ::* '''-o''' Output prefix, output file names = myoutfiles |
| | ::*'''-minMaf''' SNPs with MAF > 5% = 0.05 |
|
| |
|
| * The .qopt file contains the admixture proportions for all individuals.
| | ===Detailed Examples and Tutorial=== |
|
| |
|
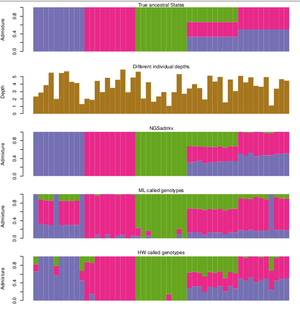
| Examples of the output files are found below.
| | Please refer to the tutorial's page [http://www.popgen.dk/software/index.php/NgsAdmixTutorial] |
|
| |
|
| | ==Citation== |
|
| |
|
| ===Log file (.log)===
| | http://www.genetics.org/content/early/2013/09/03/genetics.113.154138.full.pdf |
| <div class="toccolours mw-collapsible mw-collapsed">
| |
| Contents of the file log file
| |
| <pre class="mw-collapsible-content">
| |
| -> Dumping file: tskSim/tsk6GL.beagle.s1.log
| |
| -> Dumping file: tskSim/tsk6GL.beagle.s1.filter
| |
| Input: lname=tskSim/tsk6GL.beagle nPop=3, fname=(null) qname=(null) outfiles=tskSim/tsk6GL.beagle.s1
| |
| Setup: seed=1 nThreads=10 method=1
| |
| Convergence: maxIter=2000 tol=0.000000 tolLike50=0.010000 dymBound=0
| |
| Filters: misTol=0.050000 minMaf=0.000000 minLrt=0.000000 minInd=0
| |
| Input file has dim: nsites=100000 nind=75
| |
| Input file has dim (AFTER filtering): nsites=100000 nind=75
| |
| iter[start] like is=9299805.984931
| |
| iter[50] like is=-6531138.892608 thres=0.002800
| |
| iter[100] like is=-6528710.773349 thres=0.001289
| |
| iter[150] like is=-6528405.896951 thres=0.001211
| |
| iter[200] like is=-6528306.803820 thres=0.000420
| |
| iter[250] like is=-6528277.160993 thres=0.000546
| |
| iter[300] like is=-6528271.925055 thres=0.000033
| |
| iter[350] like is=-6528271.177692 thres=0.000008
| |
| iter[400] like is=-6528270.876315 thres=0.000005
| |
| iter[450] like is=-6528270.772894 thres=0.000140
| |
| iter[500] like is=-6528270.747721 thres=0.000002
| |
| iter[550] like is=-6528270.740654 thres=0.000002
| |
| Convergence achived because log likelihooditer difference for 50 iteraction is less than 0.010000
| |
| best like=-6528270.740654 after 550 iterations
| |
| -> Dumping file: tskSim/tsk6GL.beagle.s1.qopt
| |
| -> Dumping file: tskSim/tsk6GL.beagle.s1.fopt.gz
| |
| [ALL done] cpu-time used = 671.82 sec
| |
| [ALL done] walltime used = 114.00 sec
| |
| </pre>
| |
| </div>
| |
|
| |
|
| ===Allele frequency ouput (.fopt)===
| | Skotte, L., Korneliussen, T. S., & Albrechtsen, A. (2013). Estimating individual admixture proportions from next generation sequencing data. Genetics, 195(3), 693–702. doi:10.1534/genetics.113.154138 |
| Each column correponds to the estimated allele frequencies for each population and each line is a SNP
| |
| <div class="toccolours mw-collapsible mw-collapsed">
| |
| Example of a .fopt file for -K 3
| |
| <pre class="mw-collapsible-content">
| |
| ... | |
| 0.75331646167520038837 0.51190946588401886608 0.50134051056701267601
| |
| 0.99999999900000002828 0.80165850924934911603 0.97470665326916294813
| |
| 0.99999999900000002828 0.89560828888972687789 0.88062641752218895341
| |
| 0.99999999900000002828 0.99999999900000002828 0.86109994249930577048
| |
| 0.70560445653074521655 0.78994686954000448154 0.93076614062025020413
| |
| 0.99999999900000002828 0.88878537780630872955 0.92662857068149151463
| |
| 0.05322676762098016434 0.22871739860812340117 0.17394852600322696645
| |
| 0.00000000100000000000 0.27428885137150410545 0.19029599645013275944
| |
| 0.57086006389212373691 0.42232596591112880891 0.74080063581586474974
| |
| 0.77359733910003525281 0.47380864146016693494 0.72073560889718923939
| |
| 0.49946404159405927148 0.21684946347150244050 0.15201985942558055021
| |
| 0.41802171086717271331 0.55490556205954566504 0.85691127728452165524
| |
| 0.77095213528720529794 0.60074618451005279418 0.70219544996184157792
| |
| 0.26517850405564091787 0.48500265408436060710 0.85432254709914456914
| |
| 0.80055081986260245852 0.74423201242010783574 0.87110476762969968334
| |
| 0.30563054476851375663 0.05233529475348827620 0.25911912824038613179
| |
| 0.51084997710733415222 0.62263692178557350498 0.50738250264097506381
| |
| 0.64790272562679740442 0.91230541484222271720 0.73015721390331478347
| |
| 0.07124629651164265942 0.37896482494356753534 0.29218012479334326548
| |
| 0.00000000100000000000 0.26969100790961914038 0.28395781874856029781
| |
| 0.97074775756045073027 0.79093498372643300520 0.64006920058897498471
| |
| 0.64661948716978157048 0.84130009558421925409 0.76730057769159087933
| |
| 0.86990900887920663553 0.79410745692063922085 0.69416721874359499367
| |
| 0.34956069940263900797 0.27773038429396151860 0.25923476721423144298
| |
| 0.77739744690560164120 0.51272232330145017798 0.53888718200036844763
| |
| 0.35431569298041332150 0.20022780744715171219 0.43176580786072032980
| |
| 0.91858160919413811563 0.99999999900000002828 0.93584179237779097082
| |
| 0.90339823126358831384 0.94729687041528465308 0.84358671720630329371
| |
| 0.87068129661127857677 0.65267891763324525911 0.59315740612546075106
| |
| 0.24102496839012735319 0.42777100607917967201 0.39594098602469629533
| |
| 0.99999999900000002828 0.99999999900000002828 0.78549330115836857313
| |
| 0.15386277372522660922 0.18035502891341426146 0.26583557049163752950
| |
| 0.22456748943597096280 0.25110807159057474403 0.17244618960511531869
| |
| 0.74816053649164548922 0.54769319158907958656 0.44532166240679449398
| |
| 0.76350303696805599252 0.86547244122202959815 0.94111974586621383043
| |
| 0.40940400475566068872 0.67767095908245833513 0.40793761498610620064
| |
| 0.85389765162910868934 0.78901563183853873351 0.93614065916219291186
| |
| 0.54108661985898742763 0.61895909938546000983 0.88522763262549941654
| |
| 0.99051495581855464323 0.78855843624128341141 0.77646441702623147929
| |
| 0.51133721761171413434 0.74521610846562824637 0.32689774480116673416
| |
| 0.66618479413060949224 0.67891474309775079465 0.80762116232856140385
| |
| 0.81793598261160704865 0.77752326447671193943 0.95349025244041396565
| |
| 0.82120324647844433752 0.99999999900000002828 0.89800731971059466474
| |
| ...
| |
| </pre>
| |
| </div>
| |
| Use the "-printInfo 1" option to get the position of the lines in the fopt file if some sites have been flltered from the analysis (-minMaf, minInd, minLRT etc)
| |
|
| |
|
| ===Admixture proportion output file (.qopt)=== | | :<u>'''Bibtex'''</u> |
| Infered admixture proporsions. Each line is an individual and each column is a population.
| | :% 24026093 |
| <div class="toccolours mw-collapsible mw-collapsed">
| | :@Article{pmid24026093, |
| Contents of the qopt file # cat tsk48GL.beagle.gz.s1.qopt
| | : Author="Skotte, L. and Korneliussen, T. S. and Albrechtsen, A. ", |
| <pre class="mw-collapsible-content">
| | : Title="{{E}stimating {I}ndividual {A}dmixture {P}roportions from {N}ext {G}eneration {S}equencing {D}ata}", |
| 0.00254460532103031574 0.00108987228478324210 0.99636552239418640919
| | : Journal="Genetics", |
| 0.00000015905647541105 0.00000000100000000000 0.99999983994352459327
| | : Year="2013", |
| 0.00034770382567266174 0.02639209238328452459 0.97326020379104283275
| | : Pages=" ", |
| 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656
| | : Month="Sep" |
| 0.00000467398081877176 0.00000000100000000000 0.99999532501918120264
| | :} |
| 0.00000000907496942853 0.00585150933779484805 0.99414848158723567728
| |
| 0.00515826525767644137 0.01138897436535154552 0.98345276037697204607
| |
| 0.03914841746468285949 0.00000000100000000000 0.96085158153531713410
| |
| 0.00000000100000000000 0.00629199375758324100 0.99370800524241675866
| |
| 0.00771173022930659625 0.00000154720357311662 0.99228672256712036059
| |
| 0.00000000100000000000 0.00075135345721917719 0.99924864554278081119
| |
| 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554
| |
| 0.00000005468413042120 0.00087279924180633879 0.99912714607406327705
| |
| 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656
| |
| 0.00712941313019542066 0.00118955677574110528 0.99168103009406338710
| |
| 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554
| |
| 0.00000000100000000000 0.00165385222968000606 0.99834614677032007535
| |
| 0.00000000100000000000 0.00006297763597355473 0.99993702136402651259
| |
| 0.00519087111391381209 0.00000000100000000000 0.99480912788608621966
| |
| 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656
| |
| 0.00202872783596746379 0.00000000100000000000 0.99797127116403261393
| |
| 0.00876424336999809782 0.00949457841911990376 0.98174117821088191516
| |
| 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554
| |
| 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554
| |
| 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554
| |
| 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554
| |
| 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656
| |
| 0.01820430093358888640 0.00000694033297829119 0.98178875873343274261
| |
| 0.00351013812443964728 0.00000020340562512923 0.99648965846993520223
| |
| 0.00771897550085272680 0.00605259705033356268 0.98622842744881378252
| |
| 0.00600595292580561029 0.00000000100000000000 0.99399404607419439284
| |
| 0.01454910070242997067 0.00543457657939076105 0.98001632271817917808
| |
| 0.02567862615486414535 0.00160921436783232220 0.97271215947730349516
| |
| 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656
| |
| 0.00000000100000000000 0.00001041560507852223 0.99998958339492149960
| |
| 0.00000000100000000000 0.01383432553657116572 0.98616567346342876021
| |
| 0.00343840097404925389 0.00000000100000000000 0.99656159802595079000
| |
| 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656
| |
| 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656
| |
| 0.00051244065751142103 0.00404846039501185508 0.99543909894747661937
| |
| 0.02003953974792894652 0.00000004934009128878 0.97996041091197982897
| |
| 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554
| |
| 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554
| |
| 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656
| |
| 0.00000000100000000000 0.00000000100000000000 0.99999999799999994554
| |
| 0.02176809890633762956 0.00000000100000000000 0.97823190009366245423
| |
| 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656
| |
| 0.01563096189267457192 0.00970868396771427770 0.97466035413961116252
| |
| 0.00000000100000000000 0.00000000100000000000 0.99999999800000005656
| |
| 0.00002540964943070735 0.00000000100000000000 0.99997458935056915408
| |
| 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000
| |
| 0.99501476026684787524 0.00000000100000000000 0.00498523873315206718
| |
| 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000
| |
| 0.99520671498720802983 0.00479241730266987201 0.00000086771012207898
| |
| 0.95884374919730619435 0.00000000100000000000 0.04115624980269377842
| |
| 0.99002104218586972628 0.00000000100000000000 0.00997895681413022567
| |
| 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000
| |
| 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000
| |
| 0.99999999770925251941 0.00000000129074746013 0.00000000100000000000
| |
| 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000
| |
| 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000
| |
| 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000
| |
| 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000
| |
| 0.98980053177767901573 0.00000005577971952226 0.01019941244260143612
| |
| 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000
| |
| 0.99999785004878083416 0.00000000100000000000 0.00000214895121910354
| |
| 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000
| |
| 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000
| |
| 0.99220030909132039820 0.00000000100000000000 0.00779968990867968733
| |
| 0.99999996788621803301 0.00000000100000000000 0.00000003111378189772
| |
| 0.99736783433174225344 0.00255940950853666971 0.00007275615972113173
| |
| 0.99998096423035520708 0.00000000574461213317 0.00001903002503262207
| |
| 0.99711097909957713270 0.00288887008493822353 0.00000015081548462101
| |
| 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000
| |
| 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000
| |
| 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000
| |
| 0.99769262012085335734 0.00000000100000000000 0.00230737887914652393
| |
| 0.99999820787375570674 0.00000000433914936351 0.00000178778709493472
| |
| 0.98047422489554170166 0.00012980111977614777 0.01939597398468214523
| |
| 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000
| |
| 0.98208006049140339488 0.00000000100000000000 0.01791993850859651197
| |
| 0.97530298545159921364 0.00000000100000000000 0.02469701354840085974
| |
| 0.99657542812406740840 0.00000000100000000000 0.00342457087593254226
| |
| 0.99954556420189066834 0.00045443479810919004 0.00000000100000000000
| |
| 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000
| |
| 0.99531584565237773976 0.00410740812985130408 0.00057674621777084644
| |
| 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000
| |
| 0.99878572597704817770 0.00000000100000000000 0.00121427302295177490
| |
| 0.98571687209123504125 0.00400077401169816448 0.01028235389706666329
| |
| 0.99027397554762419674 0.00840892511494516215 0.00131709933743062008
| |
| 0.99999993504923445631 0.00000000100000000000 0.00000006395076564386
| |
| 0.95946639819101930957 0.00000000100000000000 0.04053360080898076034
| |
| 0.99999999800000005656 0.00000000100000000000 0.00000000100000000000
| |
| 0.98414939425022363029 0.01585059024074651421 0.00000001550902978739
| |
| 0.99999999622245250297 0.00000000277754757396 0.00000000100000000000
| |
| 0.99525652466242930938 0.00000001683386219288 0.00474345850370842034
| |
| 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000
| |
| 0.99999999799999994554 0.00000000100000000000 0.00000000100000000000
| |
| 0.99999965447943561792 0.00000000100000000000 0.00000034452056438734
| |
| 0.99864814059528783652 0.00135185840471215468 0.00000000100000000000
| |
| 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000
| |
| 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000
| |
| 0.00000001076370464123 0.99999998823629543399 0.00000000100000000000
| |
| 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000
| |
| 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000
| |
| 0.00000000099999999999 0.99999999799999994554 0.00000000099999999999
| |
| 0.00000000099999999999 0.99999999799999994554 0.00000000099999999999
| |
| 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000
| |
| 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000
| |
| 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000
| |
| 0.00000000099999999999 0.99999999799999994554 0.00000000099999999999
| |
| 0.00000000099999999999 0.99999999800000005656 0.00000000099999999999
| |
| 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000
| |
| 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000
| |
| 0.00000000099999999999 0.99999999800000005656 0.00000000099999999999
| |
| 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000
| |
| 0.00000000099999999999 0.99999999800000005656 0.00000000099999999999
| |
| 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000
| |
| 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000
| |
| 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000
| |
| 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000
| |
| 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000
| |
| 0.00000000099999999999 0.99999999800000005656 0.00000000099999999999
| |
| 0.00000000099999999999 0.99999999800000005656 0.00000000099999999999
| |
| 0.00000000099999999999 0.99999999799999994554 0.00000000099999999999
| |
| 0.00000000099999999999 0.99999999799999994554 0.00000000099999999999
| |
| 0.00000000099999999999 0.99999999800000005656 0.00000000099999999999
| |
| 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000
| |
| 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000
| |
| 0.00000000099999999999 0.99999999799999994554 0.00000000099999999999
| |
| 0.00000000099999999999 0.99999999799999994554 0.00000000099999999999
| |
| 0.00000000099999999999 0.99999999799999994554 0.00000000099999999999
| |
| 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000
| |
| 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000
| |
| 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000
| |
| 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000
| |
| 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000
| |
| 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000
| |
| 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000
| |
| 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000
| |
| 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000
| |
| 0.00000000099999999999 0.99999999799999994554 0.00000000099999999999
| |
| 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000
| |
| 0.00000000100000000000 0.99999999800000005656 0.00000000100000000000
| |
| 0.00000000100000000000 0.99999986659623718577 0.00000013240376283687
| |
| 0.00000000099999999999 0.99999999799999994554 0.00000000099999999999
| |
| 0.00000000099999999999 0.99999999799999994554 0.00000000099999999999
| |
| 0.00000000100000000000 0.99632783404679736705 0.00367216495320256799
| |
| 0.00000000100000000000 0.99999999799999994554 0.00000000100000000000
| |
| 0.00000000099999999999 0.99999999800000005656 0.00000000099999999999
| |
| 0.35919621347731411909 0.32381633362411937904 0.31698745289856661289
| |
| 0.31048363757756514136 0.30902410742704566893 0.38049225499538924522
| |
| 0.36341140678787386964 0.33678307361394943520 0.29980551959817652863
| |
| 0.34550713774447228133 0.34037087985425079628 0.31412198240127681137
| |
| 0.34705579219215104692 0.35218792485566730033 0.30075628295218165276
| |
| 0.33646039412306782967 0.32632754139618752598 0.33721206448074481088
| |
| 0.31881401220765009930 0.34885621407165418040 0.33232977372069577582
| |
| 0.34999374672052624424 0.33030931848049555066 0.31969693479897826061
| |
| 0.33152251818028721786 0.32339147992992234304 0.34508600188979043910
| |
| 0.31959998197389311025 0.33152491237148390413 0.34887510565462298562
| |
| 0.34724548642936803322 0.31809475756470984020 0.33465975600592196004
| |
| 0.33378069767858009609 0.33223636639277298599 0.33398293592864686241
| |
| 0.32023090400419051971 0.33179989332826043125 0.34796920266754916007
| |
| 0.35205158009776410521 0.33547091017851976558 0.31247750972371612921
| |
| 0.34291063455495451873 0.31853488093100223999 0.33855448451404313026
| |
| 0.31929132670383747472 0.32755905579808902717 0.35314961749807355362
| |
| 0.34114474726121107873 0.34607065583774476725 0.31278459690104404300
| |
| 0.33725705347681012025 0.32910919226619778089 0.33363375425699209886
| |
| 0.33918213722968154622 0.32278745806952213737 0.33803040470079642743
| |
| 0.33788659799509024317 0.34692305448657090317 0.31519034751833896468
| |
| 0.35876135180876589370 0.33843260979944000955 0.30280603839179404124
| |
| 0.34721570614318736370 0.34395335873604998556 0.30883093512076259524
| |
| 0.34165097731337079612 0.32814110943000784903 0.33020791325662146587
| |
| 0.33922542743931027864 0.32639619830977489867 0.33437837425091476717
| |
| 0.34461619391735059947 0.33133174331942943924 0.32405206276321996128
| |
| 0.34277551565686120716 0.32746953398981676342 0.32975495035332202942
| |
| 0.33842982221926010133 0.31224638933762871584 0.34932378844311123833
| |
| 0.34443810815667752490 0.32640113997211872565 0.32916075187120380496
| |
| 0.31723258569943768581 0.34955203711397470068 0.33321537718658750249
| |
| 0.35394053250677920408 0.33291498389624818444 0.31314448359697255597
| |
| 0.33504517457864940733 0.34188143503173562543 0.32307339038961496724
| |
| 0.33240938202788244960 0.34671459781042585080 0.32087602016169164409
| |
| 0.31745792352948248860 0.33722730677636020280 0.34531476969415725309
| |
| 0.33098224522913716195 0.33312298285105168549 0.33589477191981131909
| |
| 0.34090909280056919117 0.32423671881295645925 0.33485418838647434958
| |
| 0.32985465610121944557 0.32124851771265583444 0.34889682618612483100
| |
| 0.33525528582568764335 0.31967441393853385234 0.34507030023577844879
| |
| 0.33823045943274382408 0.33932114218381809190 0.32244839838343819505
| |
| 0.34374166546335593875 0.33527470302709477812 0.32098363150954922762
| |
| 0.32177399566214615056 0.34277626859597382092 0.33544973574188002852
| |
| 0.34915111840878915173 0.33072079898488659921 0.32012808260632419355
| |
| 0.31132788816691708833 0.32844185942225745389 0.36023025241082540227
| |
| 0.33067206673512555826 0.34601992411426535368 0.32330800915060908807
| |
| 0.31337643746173032833 0.33835721859074846529 0.34826634394752131740
| |
| 0.32762993090356395953 0.34856645453438306337 0.32380361456205303261
| |
| 0.33558678075595765877 0.34449062515269568419 0.31992259409134682357
| |
| 0.33433652456352996873 0.32868556951924504661 0.33697790591722515119
| |
| 0.32115036446030281736 0.35050069566489522321 0.32834893987480190392
| |
| 0.32524569843140932468 0.33953480032298033464 0.33521950124561045170
| |
| 0.33520046917246110185 0.31124301814705779279 0.35355651268048110536
| |
| 0.51565151014669796670 0.00027180960956305278 0.48407668024373901039
| |
| 0.51978922685130035664 0.01333903580405943964 0.46687173734464021413
| |
| 0.48123878312258933088 0.00648941795451128591 0.51227179892289931296
| |
| 0.48941833241028537271 0.00512373007237581363 0.50545793751733880672
| |
| 0.48421136927686320162 0.00600153379448644612 0.50978709692865020742
| |
| 0.53246468447754891073 0.00000000100000000000 0.46753531452245111755
| |
| 0.50637710620505416159 0.01564455874020675985 0.47797833505473913407
| |
| 0.49416813414210103428 0.00000000100000000000 0.50583186485789899400
| |
| 0.51328206693115174808 0.00000000100000000000 0.48671793206884833571
| |
| 0.50420356848059588728 0.00779539942445491366 0.48800103209494921641
| |
| 0.51589943710654184716 0.00000000100000000000 0.48410056189345807010
| |
| 0.46643393286795947761 0.00024627960390510270 0.53331978752813535838
| |
| 0.50134326603627110686 0.00000000100000000000 0.49865673296372897694
| |
| 0.52516062216154979492 0.00887494007947397384 0.46596443775897622430
| |
| 0.50553300231497877437 0.00610541400596737328 0.48836158367905380118
| |
| 0.48505848053244243756 0.00412236953776635561 0.51081914992979127188
| |
| 0.50419106430093152404 0.00671707921410998055 0.48909185648495850929
| |
| 0.51266037905765671212 0.00565931340437971983 0.48168030753796364785
| |
| 0.50479638826213368841 0.00082364200405335279 0.49437996973381287402
| |
| 0.48963785250324892706 0.00000000100000000000 0.51036214649675115673
| |
| 0.49861342640726780129 0.00000000100000000000 0.50138657259273211597
| |
| 0.49321745088202589846 0.00000000100000000000 0.50678254811797418533
| |
| 0.52297921048641760056 0.00000000100000000000 0.47702078851358242773
| |
| 0.51351947193443381323 0.00000000100000000000 0.48648052706556610403
| |
| 0.49861600587139209839 0.01143470350387426789 0.48994929062473369097
| |
| 0.47497824395255133778 0.00413641430709298184 0.52088534174035572288
| |
| 0.50602874958787047444 0.00000013752429825494 0.49397111288783129845
| |
| 0.51347175918678078510 0.00477133273041653854 0.48175690808280269284
| |
| 0.50359809216181616875 0.00000002299679746021 0.49640188484138642044
| |
| 0.52201190781479689385 0.00000000100000000000 0.47798809118520296790
| |
| 0.52427554763933403859 0.01637369304678280152 0.45935075931388308357
| |
| 0.50464335890649447691 0.01062810063722730188 0.48472854045627822295
| |
| 0.48795095623978190780 0.00032508303858300066 0.51172396072163517378
| |
| 0.49273360783177866384 0.03185613233234574349 0.47541025983587564818
| |
| 0.49075081269029041664 0.00043182816413278401 0.50881735914557668643
| |
| 0.51236233643387329995 0.01050799870797843559 0.47712966485814828355
| |
| 0.51939186110717183720 0.00638063180499700081 0.47422750708783106832
| |
| 0.49685157861691658931 0.00000000100000000000 0.50314842038308338346
| |
| 0.50376251978896124939 0.00609062514993390959 0.49014685506110500235
| |
| 0.50469879197514677660 0.00000000100000000000 0.49530120702485330719
| |
| 0.48806858812981018803 0.00000000100000000000 0.51193141087018978475
| |
| 0.49345173654735252633 0.00767168036095551131 0.49887658309169191639
| |
| 0.51926063211476558568 0.00000000100000000000 0.48073936688523438709
| |
| 0.49182360714466144547 0.00000000100000000000 0.50817639185533869384
| |
| 0.50012065040991493525 0.00101172020552988784 0.49886762938455525562
| |
| 0.49490771372946151807 0.00000000100000000000 0.50509228527053839919
| |
| 0.50981594186492362741 0.01168450085559137597 0.47849955727948501050
| |
| 0.48459184220397827358 0.00000007440008454733 0.51540808339593724430
| |
| 0.51153925961371649045 0.00045999176804108893 0.48800074861824249695
| |
| 0.49380129779182529992 0.00214174101547949525 0.50405696119269527422
| |
| 0.10504303642339951619 0.45848347542219436423 0.43647348815440606407
| |
| 0.09383999674587484296 0.44580529318052469767 0.46035471007360045936
| |
| 0.11801124345951279071 0.44619343422410290279 0.43579532231638429263
| |
| 0.10150817897299509174 0.44474184109029252232 0.45374997993671234431
| |
| 0.14144944553914898244 0.47426718065022838156 0.38428337381062249722
| |
| 0.08656596263718574491 0.47201374694852676894 0.44142029041428754166
| |
| 0.10422682420288104099 0.45665008652196642513 0.43912308927515242285
| |
| 0.07422281507005458467 0.46668026430253822801 0.45909692062740725671
| |
| 0.11152984148911383733 0.44326164444242566187 0.44520851406846068121
| |
| 0.12101900721666984662 0.45534926548479054409 0.42363172729853953991
| |
| 0.19287147372937366030 0.40220634979635128126 0.40492217647427497518
| |
| 0.19868166550667537562 0.39952077624337684059 0.40179755824994778379
| |
| 0.20144056442189406386 0.40552701281654912613 0.39303242276155692103
| |
| 0.17400131741109717276 0.41572345587205422612 0.41027522671684846234
| |
| 0.19363830614785534912 0.39941552029693161430 0.40694617355521295332
| |
| 0.20932370419936904837 0.41063785306931777086 0.38003844273131326403
| |
| 0.21496306930156286463 0.41077627378883840858 0.37426065690959875454
| |
| 0.20887311245081657818 0.39219787302656328176 0.39892901452262014006
| |
| 0.18789467459437667052 0.42880445734573224836 0.38330086805989094234
| |
| 0.21467435158258502126 0.41396326091136687042 0.37136238750604805281
| |
| 0.30215275924600598634 0.35114326369103593395 0.34670397706295807971
| |
| 0.27985580964526363124 0.36766711333486662427 0.35247707701986974449
| |
| 0.29214764907998119758 0.34353124024041165052 0.36432111067960715189
| |
| 0.28098186396660507214 0.35436535705487937076 0.36465277897851555711
| |
| 0.29909659519210785028 0.34708664349540557792 0.35381676131248662731
| |
| 0.29960230758566036569 0.34764467237891033546 0.35275302003542929885
| |
| 0.28690707484319816212 0.36958476358894237768 0.34350816156785934918
| |
| 0.31218824558522878521 0.35988855578362860532 0.32792319863114272049
| |
| 0.29371283648699086921 0.34536893102077848017 0.36091823249223065062
| |
| 0.32028624797598659324 0.35059182523172049972 0.32912192679229296255
| |
| 0.39315538655109805166 0.30778919233772789044 0.29905542111117405790
| |
| 0.39625700997625840083 0.29350948690034872612 0.31023350312339292856
| |
| 0.40087160410050781678 0.31851581382017457589 0.28061258207931755182
| |
| 0.40117357253398744366 0.30569836130272198815 0.29312806616329067921
| |
| 0.40013703551439627759 0.28691859513594913933 0.31294436934965452757
| |
| 0.39131222513930874474 0.30759794867682349606 0.30108982618386764818
| |
| 0.40826221599444090238 0.30658973748486684219 0.28514804652069231095
| |
| 0.41420080477834714250 0.28227625784283560950 0.30352293737881719249
| |
| 0.39119930707342420728 0.32102763805993583812 0.28777305486664006562
| |
| 0.37635520411942069430 0.29805329179310008358 0.32559150408747933314
| |
| 0.51400585200303006150 0.26100245041580294458 0.22499169758116702167
| |
| 0.50336119658518030384 0.25110166586697690860 0.24553713754784287082
| |
| 0.47299237773462793344 0.26084178003823194070 0.26616584222714018138
| |
| 0.49359314224598493936 0.26013978211456978418 0.24626707563944530421
| |
| 0.52795469779405246324 0.26499345968140075591 0.20705184252454675309
| |
| 0.48219467330650939152 0.25987283477635270135 0.25793249191713785162
| |
| 0.47626160019217189667 0.25351817092177358903 0.27022022888605456981
| |
| 0.51617477226059282902 0.23162353057460718930 0.25220169716479995392
| |
| 0.49698887507445854705 0.24557159475841641716 0.25743953016712495252
| |
| 0.52733914260860248469 0.25309832534801629533 0.21956253204338116447
| |
| 0.56749881833694781896 0.19172441472755546998 0.24077676693549673881
| |
| 0.59339160859286765870 0.19241414198845174788 0.21419424941868048240
| |
| 0.62308540846251914136 0.18054125203843729430 0.19637333949904353658
| |
| 0.59485531592769125275 0.20909554531024135415 0.19604913876206744860
| |
| 0.61310545246842529377 0.20645329445333451823 0.18044125307824007698
| |
| 0.60102956519838679483 0.21237444166376903687 0.18659599313784405727
| |
| 0.59278179178128642679 0.20826418834431797977 0.19895401987439562119
| |
| 0.60456224253100432353 0.20686687908046738626 0.18857087838852840123
| |
| 0.59417710257213784963 0.21264514488765640099 0.19317775254020574938
| |
| 0.59059286756608764257 0.21451811369415349495 0.19488901873975889023
| |
| 0.69484036887292865980 0.14634823390637874407 0.15881139722069256837
| |
| 0.69945423984127830241 0.16333221995631252987 0.13721354020240922322
| |
| 0.69115689116107958956 0.14927316115273414621 0.15956994768618620872
| |
| 0.68851717088680941536 0.14201541767923545057 0.16946741143395496754
| |
| 0.69288781352263861812 0.14270021794166909412 0.16441196853569234326
| |
| 0.68819873910998985433 0.16242980538224471854 0.14937145550776548264
| |
| 0.68619763716276405141 0.14370194479775053042 0.17010041803948539041
| |
| 0.68596343194490616568 0.16051691534743553480 0.15351965270765843830
| |
| 0.70684340251150390433 0.16654037983665334610 0.12661621765184280508
| |
| 0.70657158115262697073 0.14984891346689468983 0.14357950538047842270
| |
| 0.79161214498168253062 0.10430887542937690438 0.10407897958894059276
| |
| 0.79477141808375573184 0.10274451187208989700 0.10248407004415439892
| |
| 0.80425538032447896342 0.10720945367236509038 0.08853516600315590457
| |
| 0.79445836435866723502 0.11481368508653701233 0.09072795055479568327
| |
| 0.80626524450581027459 0.08599284906042292675 0.10774190643376663212
| |
| 0.77991736902186048486 0.08777798585427237787 0.13230464512386716502
| |
| 0.77897241390666871474 0.11419808069913564563 0.10682950539419577840
| |
| 0.80225596727756287585 0.10739115862914316857 0.09035287409329402497
| |
| 0.81035643868218754093 0.11405964018980654928 0.07558392112800596530
| |
| 0.80474324803558927588 0.09992219310105134034 0.09533455886335934215
| |
| 0.89147290804053958002 0.05818869713285088757 0.05033839482660958098
| |
| 0.87135519951168793895 0.04885203404408157424 0.07979276644423052844
| |
| 0.90273220877706750187 0.05642671780738096193 0.04084107341555152232
| |
| 0.90299890240805003039 0.05982401615206547896 0.03717708143988454617
| |
| 0.88622329583732417646 0.03227381365259313073 0.08150289051008267893
| |
| 0.89149278212958615875 0.03556871666107842139 0.07293850120933542680
| |
| 0.90540444756330573650 0.06637446770308205735 0.02822108473361228942
| |
| 0.89581315874618450135 0.06675457610008654619 0.03743226515372900798
| |
| 0.86941364504212315101 0.03330392614486758773 0.09728242881300920575
| |
| 0.88098981477392690476 0.04673780362475228600 0.07227238160132080924
| |
| </pre>
| |
| </div>
| |